"Dysleksja cyfrowa", NLD, dyskalkulia rozwojowa, procesy przetwarzania liczb i liczenia
Wprowadzenie
Rozwojowa dyskalkulia stanowi, podobnie
jak dysleksja, jedną z wielu trudności w uczeniu się. Jest jednak rzadziej przedmiotem
zainteresowania badaczy. Przykładem bogatego pod względem merytorycznym
opracowania na temat rozwojowej dyskalkulii jest artykuł Michaela Von Astera
z Uniwersytetu w Zurichu, zamieszczony w jednym z nowszych numerów "European
Child and Adolescent Psychiatry". W artykule znajdziemy nie tylko definicje, ale także mniej znane teorie mające zastosowanie w wyjaśnianiu procesów przetwarzania liczby i liczenia (np. teorię minimalnej kognitywnej/poznawczej architektury M. Andersona z 1992 roku, czy też modelu trójkodowego Dehaene). Ponadto
Autor komentuje badania własne a ich wyniki umożliwiają wyodrębnienie trzech
podtypów rozwojowej dyskalkulii. W opracowaniu znajdziemy także ciekawe
studium indywidualnego przypadku 17-latka ujawniającego rozwojową dyskalkulię.
Modele neuropsychologiczne odwołują się do reprezentacyjnych i specyficznych ze względu na format modułów, zlokalizowanych w różnorodnych obszarach lewej i prawej półkuli mózgowej. Moduły te odnoszą się do poznawczego przetwarzania liczb i dokonywania obliczeń. Najszerzej dyskutowane modele to: model McCloskey i współpracowników, model trój-kodowy Dehaene oraz teoria złożonego kodowania
Campbella i Clark. Modele te opierają się na obserwacjach dysocjacji i podwójnych dysocjacji w procesach przetwarzania liczb i dokonywania obliczeń u dorosłych z uszkodzeniem mózgu. Niektóre aspekty tych modeli pozostają kontrowersyjne.
Mając na względzie klasyfikacje syndromu NLD, należy podkreślić, że wielu badaczy opisywało podtypy rozwojowej dyskalkulii (ang. developmental dyscalculia) i próbowało odnosić te specyficzne kognitywne zaburzenia do dysfunkcji powiązanych z niedojrzałością różnych modułów i odpowiadającym im obszarów rozwijającego się mózgu (por. M. von Aster, 2000).
Patrząc na syndrom NLD z terminologicznego punktu widzenia trzeba być świadomym tego, że według ICD - 10 oraz DSM - IV głównym
kryterium definicyjnym DD jest istotna rozbieżność między specyficznymi
zdolnościami matematycznymi a ogólną inteligencją. Ważnym dla dyskalkulii faktem jest to, że porównując dzieci z DD z dziećmi bez DD, matematyczne zdolności u dzieci z DD znajdują się na poziomie oczekiwanym w stosunku do dzieci mających normalne osiągnięcia, ale znajdujących się w młodszym wieku. Oznacza to, że dzieci z DD ujawniają różnicę między ich wiekiem umysłowym a wiekiem życia w zakresie zdolności przetwarzania liczb
i liczenia. Kluczowa rola inteligencji psychometrycznej w definiowaniu
kryteriów zaburzeń rozwojowych sprawia, że niezbędne jest bliższe przyjrzenie
się współczesnym teoriom inteligencji w celu opracowania teoretycznego modelu.
Współczesna rozwojowa teoria inteligencji, która odnosi się w szczególności do zaburzeń rozwojowych takich jak dysleksja, to teoria M. Andersona (M. von Aster, 2000). Według jego teorii, różnice w ogólnym funkcjonowaniu poznawczym (wyrażone za pomocą wyniku I.I. w pełnej skali) między dziećmi w tym samym wieku są spowodowane różnicami w zakresie zdolności przetwarzania podstawowych informacji. Różnice te polegają głównie na szybkości przetwarzania podstawowego materiału i pozostają stabilne wraz z postępującym rozwojem. Natomiast różnice w zakresie zdolności poznawczych między dziećmi w różnym wieku są przypisane różnicom w zakresie dojrzewania specyficznych funkcjonalnych modułów mózgu, które
wyłaniają się na pewnych etapach rozwojowych i są albo filogenetycznie
ukształtowane albo ontogenetycznie nabyte przez intensywne ćwiczenie w
zależności od potrzeb i wymagań środowiskowych (aspekt doświadczenia poznawczego).
Teoria Andersona o minimalnej poznawczej strukturze (kognitywnej mikro-strukturze) zapewnia użyteczny model dla dokonania syntezy różnych,
czasami sprzecznych wyników dotyczących DD i innych trudności w uczeniu
się oraz do wyjaśnienia różnorodnych genetycznych, powiązanych z płcią
oraz środowiskowych (kulturowych, socjo-emocjonalnych, wychowawczych) wpływów,
które okazało się, że miały udział w różnicach dotyczących zdolności poznawczych
u dzieci(M. Von Aster, 2000).
Dyskalkulia rozwojowa. Deficyty w zakresie modularyzacji i lateralizacji w odniesieniu do zdolności przetwarzania liczb i liczenia
Dysocjacje, podtypy, modele poznawczego funkcjonowania, lokalizacjaNa podstawie badań funkcjonalnych mózgu wiemy, że różnorodne aspekty złożonych zdolności poznawczych (tj. przetwarzania językowego lub numerycznego) są bez wątpienia reprezentowane w różnorodnych obszarach ludzkiego mózgu. Co więcej, można udowodnić, że reprezentacja korowa pewnej zdolności różni się w zależności
od czasu, w którym ta zdolność została nabyta. Kim i in. (za: M. Von Aster,
2000), na przykład, stosując funkcjonalny rezonans magnetyczny,
porównali osoby dwujęzyczne podczas przetwarzania językowego, które we
wcześniejszym i późniejszym wieku przyswoiły drugi język. U osób, które
nabyły drugi język po ukończeniu 11 roku życia (późniejsze osoby dwujęzyczne),
zanotowano znaczące różnice między różnymi obszarach w okolicy Broca, które zwiększały się
podczas przetwarzania językowego w pierwszym i drugim języku. Natomiast dwujęzyczne osoby, które nabyły drugi język w pierwszych latach życia ("wcześniejsze osoby dwujęzyczne"),ujawniły brak takich rozbieżności w tych samych obszarach mózgu w okolicy Broca.
Dehaene i in. zbadali modele czynności
funkcjonalnych mózgu u dorosłych podczas wykonywania różnych zadań liczbowych. Podczas wykonywania zadań, które wymagały dokładnych obliczeń optymalna aktywność miała miejsce w lewej, dolnej okolicy przedczołowej kory mózgowej.
Dehaene i koledzy twierdzą, że wyniki
potwierdzają istnienie co najmniej dwóch spośród trzech modeli,
które stanowią model trójkodowy lub też potrójnego kodu (Rys.1) dla przetwarzania liczb, a mianowicie
modelu, w którym liczby są reprezentowane jako słowa-liczby (werbalny
wyrazowy, słowny charakter liczby) oraz modelu, w którym liczby są wyobrażane jako analogiczne miejsce
na zewnętrznej osi liczbowej (wyobrażenie analogicznej wielkości liczbowej).
Rys.1 Model trój-kodowy, potrójnego kodu autorstwa Dehaene dla kognitywnych aspektów liczbowych
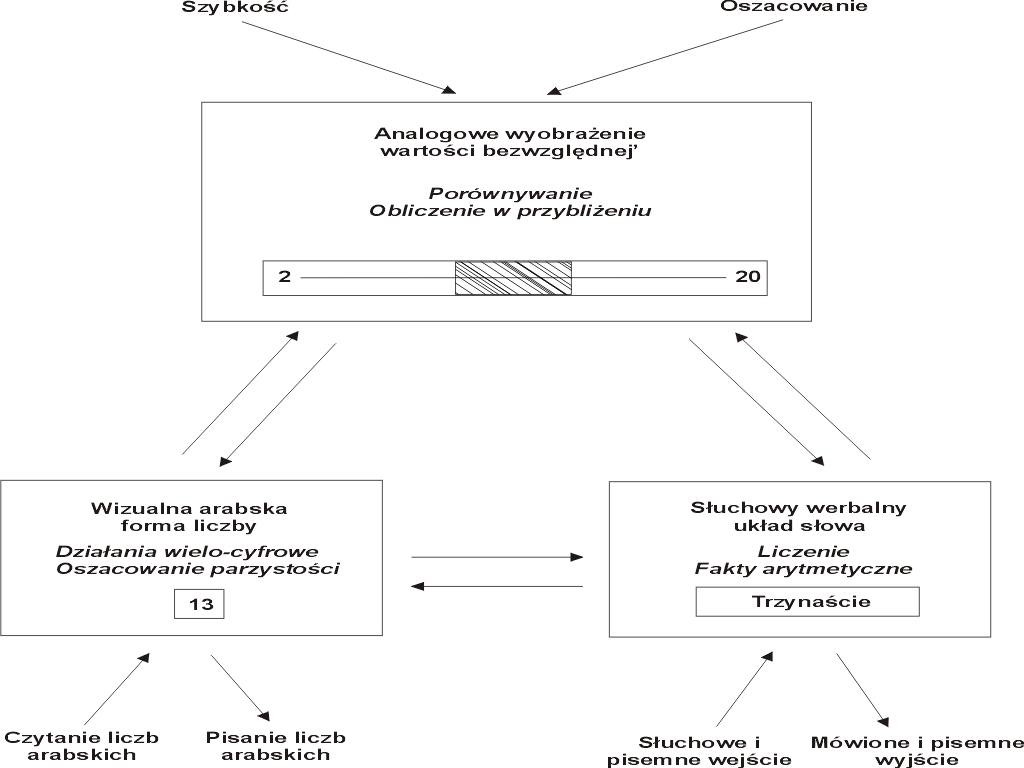
W obrębie modelu trój-kodowego lub modelu potrójnego kodu, zdolności
takie jak zaokrąglanie, dokonywanie obliczeń w przybliżeniu i porównywanie liczb są przypisane analogicznemu
modelowi, w którym zdolności takie jak liczenie, wykorzystywanie procedur
liczenia w dodawaniu i odejmowaniu oraz przywoływanie z pamięci faktów matematycznych,
umieszczono na modelu werbalnym. Działania na wielu cyfrach i liczbach oraz oszacowanie
parzystości liczby są możliwe do wykonania, według założeń tego modelu, w obrębie trzeciego modułu, przybierającego kształt liczby arabskiej, w którym liczby są reprezentowane przez ich
zapis w piśmie arabskim czyli przez cyfry arabskie (np.1, 2, 3 itp., a nie I, II, III). Te trzy moduły stanowią system przetwarzania liczby i dokonywania obliczeń,
w którym poszczególne moduły są autonomiczne, współzależne oraz aktywizowane
w zależności od potrzeb, czy wymagań stawianych przez dane zadanie arytmetyczne.
Dysocjacje oraz podwójne dysocjacje
poszczególnych zdolności przetwarzania liczby i zdolności kalkulacyjnych,
które zostały w szerokim zakresie opisane u dorosłych z uszkodzonym mózgiem,
zostały tylko zaobserwowane w kilku przypadkach u dzieci z DD. Na przykład,
Temple (za: M. Von Aster, 2000) zanotował rozwojowe zaburzenie przetwarzania
liczby nazwane dysleksją cyfrową u 11-letniego chłopca, który cechował
się dostosowanymi do jego wieku życia umiejętnościami czytania i pisania, ale uczeń ten był
niezdolny do właściwego odczytywania cyfr arabskich oraz właściwego zapisywania
wypowiadanych na głos cyfr arabskich. Co więcej, nie był on w stanie poprawnie odczytać
i zapisać wyrazów, słów oznaczających liczby, pomimo dobrze ukształtowanych umiejętności w
zakresie czytania, co wskazuje na istnienie niezależnych modułów dla leksykalnego
i syntaktycznego przetwarzania zarówno liczb arabskich, pisanych
jak i wymawianych na głos. W badaniach zaobserwowano również dzieci, które miały zadowalające osiągnięcia
w czytaniu i pisaniu liczb w różnych formatach, postaciach, ale ujawniały poważne trudności
w przywoływaniu faktów arytmetycznych z pamięci (dyskalkulia faktu - liczby)
lub w stosowaniu arytmetycznych procedur, pomimo poprawnego zrozumienia
funkcji pełnionej przez pojęcia matematyczne w działaniach na liczbach (rozwojowa proceduralna dyskalkulia). Przypadki,
o których mowa, potwierdzają pewne elementy modelu McCloskey i współpracowników
(Rysunek 2), a w szczególności udowadniają istnienie modułów dla wiedzy typu liczba-
fakt oraz wiedzy proceduralnej (M. Von Aster, 2000).
Rys. 2. Model przetwarzania liczby
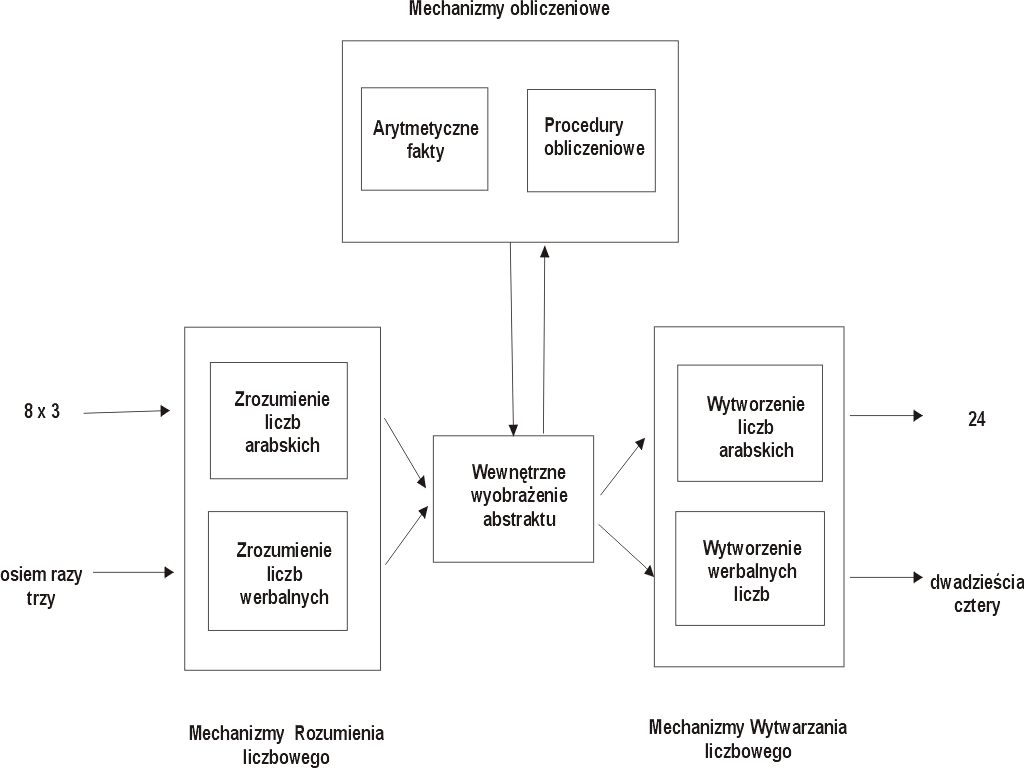
Różnorodne podtypy DD są także powiązane
z dysfunkcją lewej lub prawej półkuli, deficytami w zakresie zdolności matematycznych, przetwarzania fonologicznego lub wzrokowo - przestrzennego.
Geary (za: M. Von Aster, 2000),na
przykład,określił dwa podtypy dyskalkulii w zależności od dysfunkcji lewej półkuli: podtyp pamięciowy z niską częstotliwością odtwarzania faktu arytmetycznego, często powiązany z trudnościami w czytaniu, oraz podtyp proceduralny z częstym stosowaniem niedojrzałych procedur i opóźnieniem w rozumieniu pojęć matematycznych. Dysfunkcja prawej
półkuli zdaniem Geary, odnosi się do "podtypu wzrokowo - przestrzennego",
powiązanego z wysoką częstotliwością błędów, które wskazują na niewłaściwe
interpretacje przestrzennie przedstawionej informacji numerycznej, takiej
jak położenie, pozycja wartości liczbowej na osi liczbowej.
Rourke i współpracownicy (za: M. Von Aster,
2000) określili podtypy zaburzeń uczenia się u dzieci na podstawie mocnych i słabych stron uczniów. Opracowali oni dwa podtypy uczniów cechujących się deficytami w zakresie
umiejętności matematycznych.
Podtyp RS zawiera dzieci, które ujawniają niskie osiągnięcia w matematyce i jeszcze słabsze zdolności w zakresie czytania i pisania. Podtyp "A", zwany także niewerbalną trudnością w uczeniu się (NLD), obejmuje dzieci, które mają dość niskie osiągnięcia w matematyce, ale ich osiągnięcia w zakresie czytania i pisania znajdują się na wystarczającym poziomie. Obie grupy ujawniły charakterystyczną rozbieżność między werbalnym I.I. i niewerbalnym I.I. Dzieci z RS ujawniły wyższe wyniki w zakresie
niewerbalnego I.I. niż werbalnego I.I., podczas gdy u dzieci z NLD było odwrotnie.
Ocena neuropsychologicznego funkcjonowania
ujawniła, że dzieci w grupie NLD mają deficyty w zakresie percepcji wzrokowo
- przestrzennej i dotykowo - kinestetycznej, a także deficyty psychomotoryczne.
Dzieci te częściej popełniają błędy w obliczeniach, a ich błędy są bardziej
nietypowe i osobliwe niż wśród dzieci zaliczonych do grupy RS.
Badacze stwierdzili u dzieci z grupy RS: dobrą percepcję wzrokowo - przestrzenną i dotykowo - kinestetyczną oraz deficyty w zakresie percepcji i pamięci słuchowej a także przetwarzania werbalnego, językowego.
Rourke i współpracownicy (za: M. Von
Aster, 2000) przypisali deficyty dzieci w grupie RS funkcjonalnym zaburzeniom
lewej półkuli, a te występujące u dzieci z grupy NLD, zaburzeniom prawej
półkuli mózgowej. Badania przeprowadzone przez Mattson i in. potwierdzają
hipotezę komplementarnych dysfunkcji lateralizacji leżących u podłoża różnorodnych
podtypów zaburzeń arytmetycznych w okresie dzieciństwa. Autorzy przebadali
czynność elektroencefalografu (36 - 44 Hz) u dzieci z dysleksją, dzieci
z zaburzeniami arytmetycznymi oraz z grupy kontrolnej, podczas rozwiązywania kognitywnych zadań werbalnych i niewerbalnych. Dzieci ujawniające słabości w zakresie umiejętności czytania cechowały się mniejszą aktywnością lewej półkuli podczas wykonywania zadań werbalnych (językowych) niż dzieci ze słabościami
w zakresie arytmetyki lub dzieci z grupy kontrolnej. Przy wykonywaniu
zadań niewerbalnych, bezsłownych dzieci wykazujące słabość w arytmetyce manifestowały
mniejszą aktywność prawej półkuli niż dzieci słabo czytające lub dzieci
z grupy kontrolnej.
W przeglądzie swoich badań, Rourke
(za: M. Von Aster, 2000) sprawdził zgodność między modelem neuropsychologicznych
deficytów u dzieci z NLD i dzieci ujawniających syndrom rozwojowy Gerstmanna.
Syndrom Gerstmanna opisany po raz
pierwszy w 1930 przez Gerstmanna, zawiera cztery symptomy, które zaobserwowano
u pacjentów dorosłych ze znajdującymi się w lewej półkuli uszkodzeniami
mózgu w obszarze gyrus angularis (zawoju kątowego): akalkulia, agnozja palcowa, brak orientacji w prawej/lewej stronie ciała i dysgrafia. Dostrzeżenie tych czterech symptomów
u dzieci bez stwierdzanych wcześniej uszkodzeń mózgu nakłoniły Kinsbourne
do wyodrębnienia rozwojowego syndromu Gerstmanna. Kliniczną trafność tego
syndromu poddano ostrej krytyce, w szczególności, rozważając fakt, że funkcjonalne
zaburzenia, do których się odnosi, mogą, w wysokim stopniu, być wyjaśnione
przez towarzyszące im symptomy afatyczne, które często się pojawiają. Cały
szereg badań i klinicznych studiów przypadków ma swój udział w rozpoznaniu,
że rozwojowy syndrom Gerstmanna obserwuje się u dzieci z rozwojową dyskalkulią,
zarówno ujawniających, jak i nie ujawniających zaburzeń towarzyszących
w zakresie języka mówionego i pisanego, a także w połączeniu z pozostałymi
symptomami neuropsychiatrycznymi. Jest to, zatem, niemożliwe, aby pojedynczo
zaliczyć rozwojowy syndrom Gerstmanna do specyficznego, miejscowego, funkcjonalnego
zaburzenia mózgu. Czy powinno się stosować pojęcie komplementarnych, funkcjonalnych
zaburzeń mózgu związanych z lateralizacją dla różnorodnych podtypów zaburzeń
arytmetycznych? Wydaje się logiczne, że istnieje zaburzenie funkcji lewej
półkuli dla nie - afatycznej lub nie - dyslektycznej postaci rozwojowego
syndromu Gerstmanna oraz zaburzenie funkcji lewej półkuli dla symptomów
rozwojowego syndromu Gerstmanna z powiązanymi zaburzeniami w przetwarzaniu
językowym.
Problem z tymi pojęciami, które skupiają
się wokół podstawowych dysfunkcjonalnych procesów albo lewej albo prawej
półkuli ujawnia się głównie w tym, że obecność niewerbalnych lub werbalnych
neuropsychologicznych deficytów prawdopodobnie nie będzie dość dokładnym
predyktorem dyskalkulii rozwojowej. Share i in. byli ogólnie w stanie dokonać
replikacji wyników uzyskanych przez Rourke'a. Jednak, w przeciwieństwie
do Rourke'a i jego współpracowników, rozważyli różnice płciowe w swojej analizie
danych i stwierdzili, że dziewczynki mające "specyficzne zaburzenie arytmetyczne"
nie ujawniają oczekiwanego wzorca NLD wzrokowo - przestrzennych słabości,
a ich neuropsychologiczny wzorzec funkcjonowania nie różnił się od grupy
kontrolnej. We własnych badaniach Autora i współpracowników (M. von Aster
i in.) tylko 50 % dzieci, które spełniły kryteria diagnostyczne dla dyskalkulii rozwojowej
ujawniło wzorzec neuropsychologiczny, który był charakterystyczny dla syndromu NLD Rourke'a.
Co ciekawe, były też takie dzieci, które naprawdę ujawniły typowy wzorzec funkcjonowania
neuropsychologicznego NLD, ale pomimo to miały dobre wyniki w zakresie
matematyki.
Teoria minimalnej kognitywnej struktury, minimalnej poznawczej mikro-struktury
Teoria Andersona, która ma na celu wyjaśnienie różnorodnych indywidualnych różnic w zakresie funkcjonowania intelektualnego postuluje dwie główne drogi rozwojowe dla przyswajania wiedzy za pomocą trzech mechanizmów przetwarzania kognitywnego (rys. 3) (M. Von Aster, 2000).
Rys. 3. Teoria minimalnej kognitywnej struktury, minimalnej poznawczej mikro-struktury
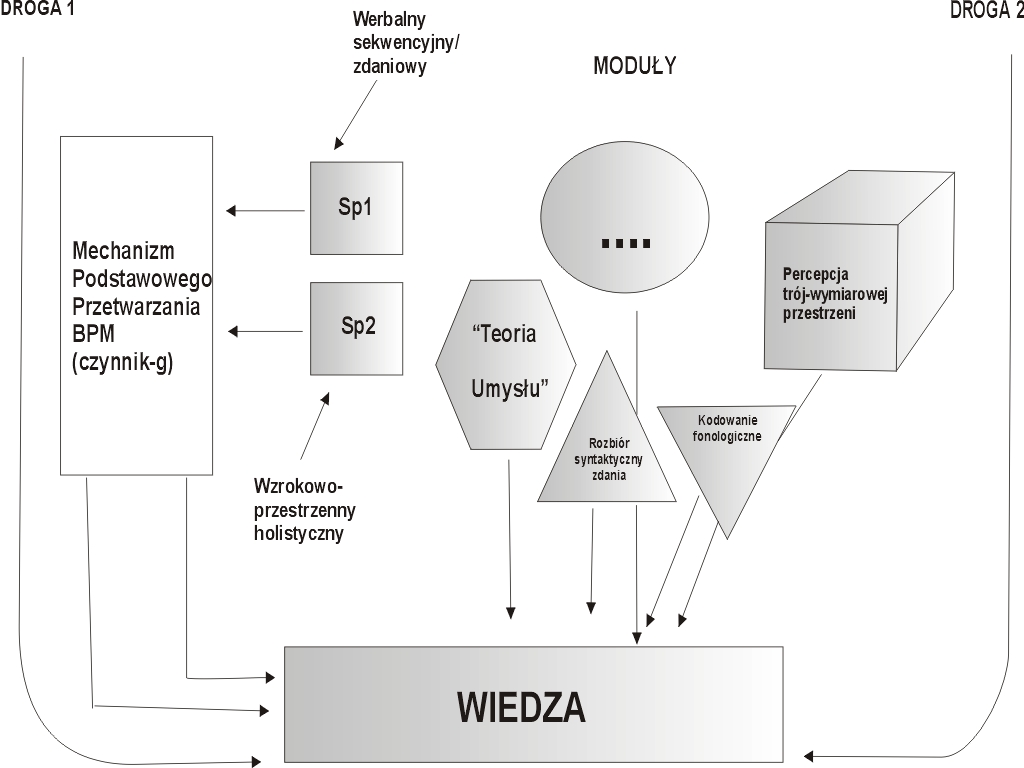
Na drodze 1, wiedza powstaje przez
myślenie, które jest aktywizowane przez mechanizm podstawowego przetwarzania
oraz dwa specyficzne procesory (SP1 i SP2), które są mechanizmami
przyswajania wiedzy wykorzystującymi dwa różne sposoby przetwarzania poznawczego.
SP1 odpowiada materiałowi sekwencyjnemu/zdaniowemu, a SP2 odpowiada materiałowi
przestrzennemu (jednoczesnemu/holistycznemu). W odniesieniu do mózgowej
lateralizacji funkcji kognitywnych, SP1 można postrzegać jako procesor
lewej półkuli, a SP2 jako procesor prawej półkuli. Mając na względzie drogę
1, indywidualne różnice są wyjaśniane różnicami w zakresie zdolności "
mechanizmu podstawowego przetwarzania" (wyrażonego ogólnym poziomem I.I.).
Im szybciej jest zdobywana wiedza, tym bardziej jest utrwalana podczas
jakiegoś okresu czasu.
Możliwe różnice w utajonej pojemności
dwóch specyficznych procesorów są psychometrycznie wyrażane przez różnice
pomiędzy werbalnym I. I. a niewerbalnym I. I., ale tylko u osób z
normalną lub dużą szybkością przetwarzania, ponieważ szybkość mechanizmu
podstawowego przetwarzania oddziałuje na stopień złożoności specyficznych dróg.
Na drodze 2, wiedza nie jest dostarczana
przez myślenie, ale szybko i automatycznie przez "moduły", które dojrzewają
w różnych okresach rozwoju człowieka. Obliczenia dokonywane za pomocą tych
modułów są niezależne od szybkości mechanizmu podstawowego przetwarzania.
Modułowe przetwarzanie jest wyszczególnione przez Andersona dla funkcji
kognitywnych takich jak percepcja przestrzeni trójwymiarowej, teoria umysłu,
syntaktyczny rozbiór zdania oraz kodowanie fonologiczne. Niektóre spośród
nich są ewolucyjnie wcześniej ukształtowane i uwarunkowane genetycznie
(np. percepcja przestrzeni trój-wymiarowej), inne na podstawie raczej ontogenetycznej,
a nie filogenetycznej, ukształtowały się przez znaczne ćwiczenie i automatyzację
podczas rozwoju, czy też poprzez doświadczenie. Ostatni przykład tej drugiej funkcji można zaobserwować w rozwoju oddzielnej korowej reprezentacji dla drugiego języka w obrębie okolicy Broca, co udokumentowano w badaniach osób dwujęzycznych.
M. Anderson dowiódł, na przykład,
że wyjątkowe umiejętności posiadane przez osoby z bardzo niskim poziomem
psychometrycznej inteligencji (osoby wybitnie zdolne) można wyjaśnić istnieniem modułów,
które są funkcjonalnie niezależne od mechanizmu podstawowego przetwarzania.
Co więcej, jego teoria wyjaśnia różnorodne formy niepowodzeń w nauce
czytania: u dzieci z niskim ogólnym poziomem zdolności, słaba zdolność
czytania (tak jak i pozostałe umiejętności szkolne) będzie miała związek
z niskim poziomem I.I. Zatem niepowodzenia w czytaniu oraz słabe osiągnięcia
szkolne są spowodowane zbyt powolnym działaniem mechanizmu podstawowego
przetwarzania. Niepowodzenia w nauce czytania mogą być także spowodowane
przez słabo rozwinięty specyficzny procesor (SP1), co w sensie psychometrycznym, obserwuje się
w postaci korelacji między zaburzeniami w czytaniu a zaobserwowaną różnicą między niskim
poziomem werbalnego I.I. i wysokim poziomem niewerbalnego I.I., o czym
pisał Rourke w podtypie RS dyskalkulii. Jednak u dzieci z przeciętnym I.I., u których nie ma takiej rozbieżności między werbalnym i niewerbalnym I.I., dysleksja także się pojawia, a zatem, może być spowodowana przez defektywny moduł dla kodowania fonologicznego (M. von Aster, 2000).
Tak jak w przypadku niepowodzenia
w nauce czytania, wydaje się, jak sądzi M. von Aster (2000), także za coś zajmującego,
umieszczenie różnych rodzajów problemów w nauce w zakresie arytmetyki i
matematyki w obrębie modelu Andersona. Objawy syndromu NLD mogą zatem odpowiadać słabo ukształtowanemu specyficznemu procesorowi dla materiału wzrokowo - przestrzennego (SP2).
Dzieci, które mają przeciętną inteligencję i nie ujawniają syndromu NLD, oraz te dzieci, które mają specyficzne problemy w manipulowaniu liczbami i dokonywaniu obliczeń matematycznych, mogą cierpieć
z powodu defektów wszystkich omawianych modułów w zakresie przetwarzania liczb i zdolności obliczeniowych.
Podtypy rozwojowej dyskalkulii. Wyniki badań prowadzonych w Zurichu
Złożoność modułowej organizacji systemu
kognitywnego przetwarzania liczby i systemu obliczeń, jak zobrazowano w
teorii neuropsychologicznej, czyni koniecznym oszacowanie różnych aspektów numerycznych. W ramach tzw. europejskiej sieci badawczej opracowano Baterię Testów Neuropsychologicznych dla Przetwarzania Liczb i Obliczania u Dzieci (NUACALC). Bateria testów NUACALC zastosowana przez M. von Astera (2000) składa się z 12 podtestów badających następujące zdolności:
Liczenie
Zdolności liczenia dzieci są uznawane za ważne warunki wstępne w procesie przyswajania umiejętności dodawania i odejmowania. W pierwszym podteście, dzieci muszą policzyć różne zbiory kropek. W odniesieniu do teoretycznego układu opracowanego przez Gelmana i Gallistela, oszacowano cztery różne podstawowe umiejętności: (i) wytwarzanie konwencjonalnej sekwencji mówionych werbalnych liczb, (ii) synchronizację pomiędzy ręcznym wskazywaniem a ustnym, werbalnym wskazywaniem, (iii) wymiar pamięci wzrokowej zadania
z rozróżnieniem między kropkami zliczonymi a tymi pozostającymi do zliczenia,
oraz, (iv) przetwarzanie ostatnio wymówionej, werbalnej liczby na odpowiadający
jej kształt arabskich cyfr.
Drugi podtest to "liczenie wstecz". Ta zdolność jest uznawana za ważną dla przyswajania strategii odliczania
wstecz podczas odejmowania. W momencie gdy odliczanie do przodu jest prototypem
automatycznych procesów kognitywnych, odliczanie wstecz za pomocą liczb-słów (liczebników)
jest kontrolowane przez system pamięci operacyjnej.
Przetwarzanie liczb
Podtesty "czytanie liczb arabskich
na głos" i "zapisywanie dyktowanych liczb arabskich" reprezentują najbardziej
powszechne procesy przetwarzania numerycznego we wczesnym wieku szkolnym. Oba zadania
bazują na takich samych (cyfry arabskie i mówione, werbalne liczby) systemach
(liczby arabskie i mówione werbalne liczby), ale zmieniają źródło i
kody obiektu. Sześć itemów każdego subtestu zostało utworzonych w odniesieniu
do właściwych czynników trudności oraz werbalnych syntaktycznych struktur.
Różne dysocjacje w reakcjach przetwarzania obserwowanych głównie u dorosłych
pacjentów z uszkodzonym mózgiem zapewniły empiryczną podstawę dla różnych
wyobrażeniowych modułów, wyszczególnionych w poprzednio wskazanych modelach
przetwarzania liczby i obliczania.
Porównanie wielkości
Dwa podtesty badają zdolności osób
do porównywania arytmetycznej wartości dwóch liczb. Liczby muszą być kodowane
właściwie według ich leksykalno - syntaktycznej struktury (lingwistycznej
i arabskiej) i muszą być oszacowywane w odniesieniu do wewnętrznej reprezentacji
ich wielkości. Różnorodne trudności zarówno dotyczące semantycznej reprezentacji/wyobrażenia (małe i duże odległości) jak i notacji (długość/wielkość liczby - słowa lub szeregu cyfr) są systematycznie wprowadzane. Wykonywanie tych zadań na niższym od oczekiwanego poziomie zanotowano w badaniach indywidualnych jak i zbiorowych u dorosłych pacjentów z uszkodzonym mózgiem, z afazją oraz z uszkodzeniem mózgu po prawej stronie.
Obliczanie w pamięci
Sześć problemów dla dodawania i odejmowanych
prezentuje się werbalnie, badając fakty liczbowe i wiedzę proceduralną
(tj. "pięć plus osiem" lub "czternaście minus sześć"). W drugim podteście
("problemy z opowiadaniem"), dzieci muszą rozwiązywać problemy dotyczące
dodawania i odejmowania zawarte w kontekście sytuacyjnym. Te cztery zadania
różnią się według poziomu trudności i rodzaju problemu (zamień, połącz
i porównaj).
Położenie liczb arabskich na analogowej osi liczbowej
Ten podtest, który zawiera pięć itemów,
ma na celu oszacowanie poziomu zrozumienia liczb i zdolności badanych
do obliczeń liczbowych, w odniesieniu do analogowego systemu reprezentacji/wyobrażenia
wielkości modelu trój-kodowego, zaproponowanego przez Dehaene.
Percepcyjne oszacowanie ilości/wielkości
Dzieci muszą oszacować liczebności/wielkości
dwóch wizualnie prezentowanych zbiorów przedmiotów (piłki i kubki).
Oszacowanie kontekstowe
Wartości semantyczne liczb zależą nie
tylko od ich arytmetycznej wartości, ale także od innych, szczególnych kontekstów.
Dzieci muszą osądzić czy, na przykład, "dziesięć liści na drzewie" lub
"osiem lamp w pokoju" to mało, trochę, czy dużo (M. von Aster, 2000).
Trzy podtypy rozwojowej dyskalkulii
- Podtyp werbalny (językowy). Dzieci ujawniające ten podtyp dyskalkulii rozwojowej mają największe trudności z liczeniem. Nie potrafią zastosować obliczeniowych procedur, aby dokonywać poprawnie obliczeń w pamięci, w szczególności w zakresie odejmowania oraz w zakresie przechowywania w pamięci faktów arytmetycznych. Większość spośród tych dzieci (9 na 11) miało dodatkowe trudności w czytaniu i pisaniu a około 50 % tych dzieci (6 na 11) miało także ADHD.
- Podtyp arabski. Dzieci ujawniające ten podtyp manifestowały poważne trudności z odczytywaniem liczb arabskich na głos oraz w zakresie zapisywania dyktowanych liczb arabskich. Wydaje się czymś prawdopodobnym, że trudności zaobserwowane w podtestach porównywania liczb (szczególnie wtedy kiedy itemy były prezentowane za pomocą cyfr) są uwarunkowane tymi problemami w przetwarzaniu, zakładając, że odnoszenie liczb do tych analogowych miejsc na osi liczbowej oraz oszacowywanie ilości nie stanowi problemu dla tych dzieci. Większość dzieci zaliczonych do podtypu, o którym mowa, miała kłopoty w nauce w obszarze matematyki. Jednak, dla więcej niż 50 % tych dzieci, niemiecki był drugim językiem.
- Podtyp głęboki, rozległy. Dzieci ujawniające ten podtyp miały poważne problemy w prawie wszystkich podtestach. Prawie wszystkie spośród tych dzieci (9 na 10) miało także trudności w czytaniu i pisaniu a większość (7 na 10) ujawniało problemy emocjonalne i w zakresie zachowania o znaczeniu klinicznym, a w niektórych przypadkach ADHD.
Mając na względzie wyniki badań przeprowadzonych
przez M. von Astera i in. (2000) można powiedzieć, że dzieci ujawniające
podtyp głęboki dyskalkulii mogą cierpieć z powodu defektywnego dojrzewania
analogowego modułu wielkości, prawdopodobnie spowodowanego przez czynniki
genetyczne lub wczesne uszkodzenie mózgu. Według Dehaene i in., moduł analogowy,
który przypuszczalnie jest wrodzony reprezentuje podstawowe "poczucie"
ilości/liczby oraz odpowiada za kodowanie semantyczne liczb. Moduł ten kształtuje się, przechodząc
od stadium przedwerbalnych, przedsłownych zdolności numerycznych (które są obecne u niemowląt)
do stadium rozwiniętego wyobrażenia wewnętrznej osi liczbowej w okresie dzieciństwa. Można przypuszczać, że dysfunkcja tego genetycznie wcześniej ukształtowanego modułu będzie hamować rozwój późniejszych zdolności matematycznych, w szczególności dojrzewania modułów reprezentacji/wyobrażeń werbalnej i arabskiej oraz powiązanego z nim przyswajania faktu liczbowego i wiedzy proceduralnej. Trudności jakich doświadczają dzieci w rozumieniu symboli liczby (słowa i cyfry) oraz we właściwym rozumieniu znaczenia wyobrażonej liczby, mogą reprezentować mechanizm przyczynowy, który prowadzi do niezdolności,
nie tylko do oszacowywania i podawania w przybliżeniu relacji, stosunków między liczbami/wielkościami,
ale także do zachowywania w pamięci liczb i tabel oraz do stosowania procedur
arytmetycznych.
Dzieci ujawniające symptomy podtypu
werbalnego, językowego i arabskiego nie miały trudności w zakresie zasadniczego "wyczucia" liczb i ilości. Są one zdolne do postrzegania i porównywania wielkości liczb do dokonywania ocen dotyczących wartości
przybliżonych oraz do tworzenia wewnętrznej analogowej linii prostej i osi liczbowej.
Dzieci z tymi rodzajami trudności mają szczególne problemy w zakresie przyswojenia,
przetwarzania i kodowania przekazywanych kulturowo systemów symboli
numerycznych (werbalnych/językowych oraz cyfr arabskich). Każdy system ma charakterystyczny
dla siebie słownik, zasady składni i określania znaczenia w zależności od różnorodnych zastosowań.
Dzieci zakwalifikowane do podtypu
werbalnego, językowego nie były w stanie liczyć dokładnie i poprawnie. Nawet jeśli
wyćwiczyły liczenie na podstawie sekwencji słów (liczebników), to popełniały często błędy w zakresie
zliczania zbiorów przedmiotów, pomijając jeden z nich, czy też licząc
jeden z nich podwójnie. Podczas rozwijania strategii liczenia dla rozwiązywania prostych zadań dotyczących dodawania i odejmowania, dzieci te mogły dokonywać błędnych obliczeń (tj. rozwiązując problem 3 + 5, nie zawsze uzyskiwały 8, ale często 7 lub 9).
W konsekwencji, strategie naprawcze oraz wiedza dotycząca liczby - faktu
nie mogła być właściwie utrwalona a dzieci polegały na czasochłonnych,
zawodnych i niedojrzałych strategiach obliczeniowych. W grupie badanej
M. von Astera (2000), 6 na 11 dzieci ujawniało zespół ADHD i miało impulsywny
i chaotyczny styl pracy, co mogło mieć swój udział w popełnianych w obliczeniach
błędach. Według naszego klinicznego doświadczenia, dzieci te będą miały
szansę na skuteczną terapię, jeśli na zespół ADHD wcześnie i z dobrym skutkiem
się oddziaływuje i nie ma żadnych zaburzeń współwystępujących z tym zespołem.
Jednak trudności w czytaniu i pisaniu tak jak zaburzenia rozwojowe mowy
i języka są także powszechne w tej grupie dzieci. W zależności
od rodzaju i nasilenia takich powiązanych zaburzeń, rozwój wypracowanych,
analogowych reprezentacji może być także zablokowany.
Dzieci w podtypie werbalnym, językowym dyskalkulii ogólnie
nie mają trudności z przyswajaniem arabskiego systemu notacyjnego oraz
w przetwarzaniu, kodowaniu cyfr arabskich na liczby werbalne i vice versa, tak jak
dzieci zaklasyfikowane do podtypu arabskiego. Większość błędów, które cechują
działania szkolne tych dzieci pojawia się w zakresie czytania liczb arabskich,
pisania liczb arabskich ze słuchu, a także w zakresie zadań kognitywnych
polegających na porównywaniu liczb, w szczególności wtedy, kiedy pary liczb
są prezentowane w postaci cyfr.
W porównaniu z normalną populacją,
dzieci posługujące się językiem ojczystym, innym niż niemiecki były nadmiernie
reprezentowane w tej grupie. Wraz z rozpoczęciem nauki szkolnej oraz systematycznym
nauczaniem arabskiego systemu notacyjnego, dzieci te muszą stosować wielorakie
zasady i procedury dla przetwarzania i kodowania liczb bazując na sekwencji liczba - słowo
języka ojczystego i języka drugiego oraz na sekwencji dwóch języków jednocześnie
oraz w oparciu o arabski system notacyjny. Może to stanowić rzeczywiste ryzyko
dla dojrzewania modułu notacji arabskiej, cyfrowej i dla przyswajania procedur arytmetycznych,
które zależą od szczególnej arabskiej reprezentacji/wyobrażenia (pisemne
obliczenia wielo-cyfrowe). Jednak, ten typ trudności w uczeniu się może
różnić się w zależności od obecności większych lub mniejszych nieprawidłowości
w słownikach liczba - słowo języków mówionych, od czasu, w którym dziecko
jest po raz pierwszy poddane wpływom drugiego języka oraz od nasilenia
tego wpływu. Byłoby czymś interesującym zbadać, czy to zjawisko jest czymś
specyficznym dla pewnych cech słowników liczba - słowo i zatem czy jest
przypuszczalnie ograniczone do specyficznych obszarów językowych (tj. niemieckiego).
Różnice międzykulturowe w zakresie czynności matematycznych pomiędzy
dziećmi pochodzącymi ze wschodniej Azji oraz dziećmi z krajów europejskich
i USA uznaje się za częściowo spowodowane czynnikami językowymi, które
faworyzują dzieci ze wschodniej Azji, ponieważ słowniki liczba - słowo
wschodnio - azjatyckie są w dużym stopniu zgodne z arabskim systemem notacyjnym.
Jeszcze jedną cechą arabskiej symboliki liczbowej jest jej czysto wzrokowo
- przestrzenna reprezentacja/wyobrażenie, mimo że dzieci z deficytami
w zakresie przetwarzania wzrokowo - przestrzennego (takimi jak brak orientacji
w lewej - prawej stronie) mogą także doświadczać trudności, na przykład
z systemem wartości miejscowych oraz z położeniem pionowym liczb (nie chodzi o położenie na osi liczbowej, w poziomie).
Studium indywidualnego przypadku 17 -letniego chłopca
Zgłoszenie przypadku
HN został zgłoszony przez swoją mamę
z powodu nasilających się u niego symptomów depresji, myśli samobójczych,
społecznego lęku, izolacji i odmowy chodzenia do szkoły. Ujawniał już od
dawna trudności w uczeniu się, które były najbardziej wymowne w obszarze
matematyki, ale także wpływały na proces czytania i pisania. HN aktualnie
dotarł do 10 roku w karierze szkolnej i przygotowuje się do podjęcia praktyki
zawodowej.
Historia przypadku
Rodzice HN rozwiedli się kiedy miał
1,5 roku. Oboje rodzice mają "przeszłość edukacyjną": ojciec miał dysleksję
o słabo nasilonych objawach podczas wczesnych lat szkolnych. Starszy brat
matki miał kłopoty z matematyką podczas edukacji w szkole podstawowej.
Nie istnieją poza tym żadne choroby psychiczne ani niepowodzenia
szkolne w tej rodzinie.
Według matki, ciąża, poród
oraz początkowa adaptacja dziecka nie budziły żadnych zastrzeżeń. HN był
spokojnym niemowlęciem z nieznacznie opóźnioną motoryką. W wieku 2,5 lat
jego mama zauważyła, że ujawnia on opóźniony rozwój językowy w porównaniu
do innych dzieci znajdujących się w tym samym wieku. W wieku 4 lat, uczęszczał
do przedszkola. Przez pierwszych kilka tygodni, HN doświadczył poważnego
lęku separacyjnego, a jego mama musiała z nim zostawać. Rok później, mama
została poinformowana, że jej syn był raczej nadpobudliwy, nieuważny, często
doświadczał ataków wściekłości oraz niszczył przedmioty, którymi się bawił.
Kiedy HN skończył 6 lat, matka przeprowadziła
się ze swoim synem z Niemiec do Szwajcarii, ale HN nigdy nie przystosował
się do językowego dialektu szwajcarsko - niemieckiego. Pierwsza konsultacja psychiatryczna
w sprawie chłopca pozwoliła na wystawienie następującej diagnozy: opóźnienie
rozwojowe, a w związku z tym, że HN miał normalny poziom intelektualny,
zalecono dostosowanie programu edukacji szkolnej w szkole masowej do jego
indywidualnych potrzeb edukacyjnych.
W wieku 7 lat, HN uczęszczał do szkoły
prywatnej z mało licznymi klasami i programem szkoły ogólnodostępnej.
Drugie badanie neuropediatryczne i psychiatryczne pozwoliło na postawienie
diagnozy: minimalna dysfunkcja mózgowa z deficytami w zakresie uwagi, kontroli
motorycznej i percepcji, a także zaburzenie hiperkinetyczne. HN zaczął
uczęszczać na psychoterapię oraz ćwiczenia z zakresu integracji sensoryczno
- motorycznej. Rok później, przeniósł się do ogólnodostępnej szkoły podstawowej,
pozostając tam przez dwa lata, ujawniając narastające problemy w uczeniu
się. Pod koniec drugiej klasy, poszerzona diagnoza psychologiczna wykazała
rozwojowe zaburzenie językowe, zaburzenie rozwojowe funkcji motorycznych,
złożone zaburzenie umiejętności szkolnych (dysleksja i dyskalkulia) oraz
zaburzenie uwagi i nadpobudliwości psychoruchowej. Uzyskano następujące
wyniki: normalny poziom intelektualny z rozbieżnością między niskimi
wynikami w skali werbalnej a przeciętnymi w skali niewerbalnej; słabe wyniki
w zakresie świadomości fonologicznej oraz pojemności pamięci werbalnej;
przeciętne wyniki w zakresie koordynacji wzrokowo - motorycznej oraz przetwarzania
wzrokowo - przestrzennego. Wyniki uzyskane za pomocą elektroencefalografu
nie ujawniły żadnych dysfunkcji.
Zgodnie z profesjonalną poradą, HN
przeniesiono do szkoły przeznaczonej dla dzieci z zaburzeniami rozwojowymi
mowy. Tam otrzymał specjalną terapię usprawniającą czytanie, pisanie a
także zdolności arytmetyczne.
Pomimo zastosowania tych różnych terapii, osiągnięcia
szkolne HN nie uległy zmianie na lepsze. W wieku 11 lat, po powtarzaniu
trzeciej klasy, uznano go za pozbawionego motywacji, nieszczęśliwego i
mającego niską samoocenę. Powiedział swojej mamie, że obawiał się innych
dzieci, że nie lubił szkoły i zaczął chodzić na wagary. Badanie foniatryczne
doprowadziło do następujących 5 diagnoz: dysnomia, brak płynności językowej,
dysleksja, dyskalkulia, dysgrafia.
Z powodu powtarzających się wagarów,
HN przeniesiono do szkoły z internatem, gdzie kontynuowano psychoterapię i terapię pedagogiczną
z zakresu czytania, pisania i matematyki oraz mowy.
W wieku 15 lat, odmówił powrotu do
szkoły z internatem po wakacjach spędzonych z mamą. Mieszkał z mamą przez
następne dwa lata i uczęszczał do klas siódmej i ósmej w szkole specjalnej
dla dzieci upośledzonych. Podczas tego okresu czasu, ponownie odmówił pójścia
do szkoły po kilku tygodniach, ponownie bał się innych dzieci, stawał się
bardziej odizolowany i nie udało mu się nawiązać żadnych znajomości. Jego
mama zaobserwowała u niego nastroje depresyjne oraz wycofanie społeczne i zamykanie się w sobie.
Badanie psychiatryczne
HN to przystojny, modnie ubrany nastolatek,
który jest w stanie nawiązać kontakt w przyjacielski i kulturalny sposób,
ale wydaje się być zakłopotany i nieśmiały. Jest leworęczny. Jego trudności
w zakresie rozumienia złożonych i dłuższych zdań w komunikacji
werbalnej nie były właściwie interpretowane z powodu dobrze rozwiniętych zdolności do niewerbalnego wyrażania siebie za pomocą gestów i mimiki oraz pełnej świadomości w zakresie tego, co zostało powiedziane i maskowania niepełnego zrozumienia wypowiedzi.
Jego zdolności werbalne oraz komunikacja uległy znacznej poprawie
wtedy, gdy tempo konwersacji było powolne a stosowane zdania, krótkie. Jego
własna ekspresja słowna wydawała się być na wymaganym poziomie. Cechowała się prostotą, mając na uwadze strukturę syntaktyczną i słownictwo. HN jest boleśnie świadomy swoich trudności
w uczeniu się i uznaje siebie za głupiego. Boi się innych nastolatków,
od dawna inni mu dokuczają i jest przekonany, że jest całkowicie nieatrakcyjny
dla innych rówieśników. Podczas ostatniego roku, często myślał o samobójstwie,
ale nie postąpił zgodnie ze swoimi myślami, mając na względzie, jaki skutek
wywarłoby to na jego matce. Żadnych objawów deficytu uwagi ani nadpobudliwości
nie zanotowano, nawet podczas badania psychologicznego.
Podsumowując, HN jest 17-letnim adolescentem
o przeciętnym poziomie ogólnej inteligencji, mającym w przeszłości trudności
w uczeniu się oraz przejawiającym niepowodzenia szkolne, który otrzymał
różnorodne formy terapii. Ma niską samoocenę, negatywny stosunek do samego siebie, fobię społeczną i jest właściwie depresyjny. Nauczył się znacznie lepiej czytać niż pisać, a na najniższym poziomie znajdują się jego umiejętności matematyczne.
Badanie przetwarzania liczbowego i zdolności obliczeniowych
HN został poddany badaniom testem EC
301 - R. Ta bateria testów zawiera 13 podtestów, które badają różnorodne
zdolności: liczenie, przetwarzanie, kodowanie liczby (mówionej, pisanej werbalnej
oraz w formacie arabskim) obliczanie w pamięci i pisemne, obliczanie w
przybliżeniu i zapamiętywanie liczb, porównywanie wielkości na liczbach
mówionych, pisanych werbalnych i arabskich, oszacowanie kontekstowe wielkości,
oszacowanie percepcyjne ilości/wielkości oraz umieszczanie arabskich i mówionych
liczb na analogowej osi liczbowej. Dodatkowo EC 301 R zawiera podtesty,
które badają wiedzę dotyczącą symboli arytmetycznych i faktów z
codziennego życia.
Wyniki
Z wyjątkiem nieznacznych trudności
z liczeniem wstecz, HN nie miał kłopotów z liczeniem i zliczaniem różnych
zbiorów kropek. Poprawnie odpowiadał na pytania dotyczące faktów
arytmetycznych z codziennego życia (tj. Ile dni ma tydzień? Ile minut ma 1 godzina?).
HN miał poważne trudności w przetwarzaniu i kodowaniu
liczb pisanych werbalnych lub prezentowanych werbalnie na notację arabską,
w szczególności wtedy, kiedy słowa - liczby zawierały więcej niż dwa elementy
(tj. werbalny mówiony: "jedenaście-tysięcy-sześć-set-trzydzieści" ? "110630",
"osiem-set-osiemnaście" ? "818"; pisemny werbalny: "pięć-tysięcy" ? "5000",
"trzydzieści-tysięcy-siedemdziesiąt-osiem" ? "30078"). Odsetek popełnianych
błędów wynosił 55 %. Był znacznie lepszy w przetwarzaniu, kodowaniu w
odwrotnym kierunku: arabskie liczby na werbalne lub pisane werbalne liczby
(15 % niewłaściwych odpowiedzi). Jednak, jego pismo odręczne było raczej
brzydkie i popełniał wiele błędów w pisaniu.
Ten wzorzec/model dysocjacji werbalnej/arabskiej
także pojawił się, kiedy HN został poproszony o porównanie dwóch liczb
według ich wielkości. Nie popełniał błędów kiedy liczby były prezentowane
w notacji arabskiej, ale miał duże trudności z
prezentowanymi werbalnie zadaniami polegającymi na porównywaniu, w których nie dał
sobie rady z 50 % zadań. Rodzaj popełnionych przez niego błędów wskazuje
na to, że jego niewłaściwe decyzje były powiązane z długością słów liczbowych
oraz z wartościami końcowych elementów (tj. "tysiąc-sześćdziesiąt-pięć"
wskazał jako liczbę większą od "trzech-tysięcy" a "siedemset-sześćdziesiąt-dziewięć"
wskazał jako liczbę większą od "dwa-tysiące-trzydzieści -pięć").
Wzorzec/model problemów transkodowania wskazuje
na to, że HN miał znacząco uszkodzone mechanizmy rozumienia liczby przekazywanej słownie,
znacznie lepsze zdolności posługiwania się liczbami w mowie oraz prawie ukształtowaną
zdolność do przetwarzania liczb arabskich. Potrafił zrozumieć i zapisywać
znaki arytmetyczne bez problemów oraz był w stanie uporządkować poprawnie
swoje pisemne obliczenia (dodawanie i odejmowanie) stosując ich pionowe położenie, tzw. słupki.
Potrafił rozwiązać pisemne wielocyfrowe zadania dotyczące dodawania i odejmowania
bez kłopotów, ale nie był w stanie rozwiązać właściwie działania stanowiącego pisemne mnożenie, z powodu mylenia stron lewa-prawa w pionowym położeniu.
W zakresie prostych, dokładnych, umysłowych
problemów obliczeniowych (dodawanie, odejmowanie, mnożenie i dzielenie),
prezentowanych słownie, a także bezsłownie, tj. cyfrowo, wszystkie z uwzględnieniem wartości
mniejszych niż 50), HN odpowiedział poprawnie na 87,5 % pytań/zadań. Błędy pojawiły
się tylko w jego odejmowaniu z pamięci (tj. "14 - 6 = 4"). Jednak, nie był w
stanie poprawnie rozwiązać prostych, arytmetycznych problemów, które zostały
zawarte w słownie zaprezentowanym sytuacyjnym kontekście (problemy z opowiadaniem).
HN odpowiedział poprawnie jedynie
na 25 % zadań, które badały obliczenia w przybliżeniu (problemy zaprezentowano
w formatach arabskich, tj. "1520 - 780 = 2300 lub 1450 lub 400 lub 700").
Poprawne odpowiedzi były tylko rejestrowane w zakresie jednego problemu
dodawania i odejmowania. Oba itemy stanowiły małe liczby z wynikami mniejszymi niż 1000. Nie udało mu się rozwiązać problemów dodawania i odejmowania w przybliżeniu, które zawierały argumenty operacji większe niż 1000; całkowicie nie dał sobie rady z problemami mnożenia i dzielenia w przybliżeniu.
HN nie popełniał błędów w
oszacowywaniu percepcyjnym ilości kontekstowej wielkości (liczby zawsze
mniejsze od 100) i mógł także odnosić arabskie oraz słowne liczby bardzo
dobrze do analogowych położeń na osi liczbowej, skończonej (od 0 do 100).
Dyskusja
HN ujawnił symptomy psychiatryczne,
które najczęściej były powiązane z rozwojową dyskalkulią: ADHD i zaburzenia
o charakterze internalizacyjnym takie jak: lęk i depresję. Jednak, podczas gdy nasilenie objawów ADHD zmniejszało się, symptomy lęku i depresji ulegały
nasileniu podczas rozwoju HN. Można przypuszczać, że zaburzenia uwagi i
słaba świadomość fonologiczna mogły utrudniać modularyzację mechanizmów
przetwarzania werbalnej liczby podczas wczesnych lat szkolnych. Doświadczanie niepowodzeń oraz poczucie bycia innym od rówieśników mogły poprzedzać zwiększanie się nasilenia objawów lęku, depresji, słabej motywacji oraz odmowy uczęszczania do szkoły, co z kolei, mogło mieć udział w słabych postępach w nauce.
Nie przeprowadzono właściwie testu psychometrycznego inteligencji. Wyniki poprzednio przeprowadzonych testów odpowiadają raczej wiernie wzorcowi, który został opisany przez Rourke'a w kontekście podtypu "RS" dyskalkulii rozwojowej (zobacz wyżej). Trudności, jakich doświadczał HN w zakresie
orientacji lewa - prawa strona ciała wraz z problemami grafomotorycznymi
wskazują także na obecność rozwojowego syndromu Gerstmanna (jednak, nie
zbadano agnozji palcowej). Podtyp RS dyskalkulii, rozwojowy syndrom Gerstmanna, rozwojowe
zaburzenie mowy oraz dysleksja uznano za reprezentujące dysfunkcje lewej
półkuli. W odniesieniu do mechanizmów teorii minimalnej struktury poznawczej
Andersona, można postulować, że HN ma słaby specyficzny procesor dla materiału
werbalnego (SP1). To, czy słaby SP1 będzie wstrzymywał dojrzewanie pewnych
modułów, czy też nie, może być interesującym, teoretycznym pytaniem dotyczącym
możliwych interakcji między różnorodnymi mechanizmami, które stanowią dwie
drogi przyswajania wiedzy w teorii Andersona. Przy założeniu o modułach
reprezentujących specyficzny format dla przetwarzania liczb, jak zaproponowano
na modelu Deheane, można przypuszczać, że rozwój dwóch modułów został zaburzony
u HN: a więc moduł werbalny i moduł analogowej wielkości liczby.
Jak wiele razy wykazywano w prezentowanym
artykule, moduł analogowej wielkości ułatwia rozpoznanie podstawowego znaczenia arytmetycznych faktów, sprzyja zrozumieniu semantyki
liczb. Przypuszcza się, że ten moduł opiera się na pierwotnie wrodzonych,
przedwerbalnych, przedsłownych zdolnościach kwantyfikacji liczbowej i jest rozumiany jako
wewnętrzna oś liczbowa, która ma charakter zmienny, a nie stały.
HN nie był w stanie utworzyć abstrakcyjnych,
analogowych wyobrażeń dla bardzo dużych liczb, z powodu ograniczonych
możliwości do przedstawiania werbalnego większych liczb oraz przypisać
poprawne nazwy do większych liczb (werbalna reprezentacja). Był on wciąż
w stanie stworzyć i powiększyć wewnętrzną oś liczbową w zakresie około 100,
uwzględniając wszystkie wartości, które mógł przedstawić werbalnie za pomocą symboli. Jednak, jego trudności w porównywaniu par ustnie prezentowanych liczb i w zaokrąglaniu
wyników arytmetycznych działań składających się z dużych liczb mogą wskazywać
na jego niezdolność do wyobrażenia i lokalizowania wewnętrznego dużych
liczb. Mówiona liczba - słowo taka jak "trzy-tysiące-osiem-set-trzydzieści-siedem"
mogą być odbierane przez HN jako niejasny splot nazw, każdy element brzmi
podobnie, ale jest za długi, by został umieszczony w jego pamięci operacyjnej,
a zatem jest identyfikowany jako szczególny symbol dla jednej, pojedynczej
liczby takiej jak: "trzy" lub "dwadzieścia-osiem". To, jednak, wydawało
by się, że jest koniecznym warunkiem aby oszacować, że "trzy-tysiące-osiem-set-trzydzieści-siedem" jest mniejsze niż "trzy-tysiące-osiem-set-trzydzieści-dziewięć", większe niż "trzy-tysiące-osiem-set-trzydzieści-cztery" oraz w przybliżeniu stanowi połowę "ośmiu-tysięcy".
HN ujawnił klasyczny wzorzec werbalnej/arabskiej
dysocjacji. Był w stanie czytać liczby arabskie (arabskie kodowanie, wewnętrzne
przesunięcie oraz werbalne wytwarzanie) oraz porównywać pary liczb arabskich,
nawet większych, poprawnie. Wydaje się, że nauczył się on zasad syntaktycznych
notacji arabskiej tak samo jak zasad kodowania całkiem dobrze. Był
także w stanie wykonywać z powodzeniem pisemne wielocyfrowe obliczenia,
mimo że nie mógł przewidzieć za pomocą oszacowania, czy wynik mógł być
logicznie poprawny, czy też nie. Miało to miejsce przypuszczalnie z powodu ograniczonych
zdolności do miejscowej lokalizacji dużych liczb na wewnętrznej osi liczbowej.
Poszerzony model rozwojowej dyskalkulii
Różnorodne podtypy
- Podtyp werbalny, językowy, słowny obejmuje zaburzenie leksykalnych/syntaktycznych werbalnych reprezentacji liczb, wykorzystanie procedur arytmetycznych o podłożu językowym (tj. strategii liczenia) oraz przywoływanie arytmetycznego faktu z pamięci.
- Podtyp arabski odzwierciedla zaburzenie w przyswajaniu drugiego "języka liczb", arabskiego systemu notacyjnego, obejmując problemy w czytaniu, pisaniu i porównywaniu liczb arabskich, na przykład przez pogwałcenie zasad syntaktycznych takich jak zasada położenia wartości miejscowej.
- Podtyp głęboki, rozległy obejmuje deficyt podstawowych, semantycznych pojęć liczby i liczebności, co implikuje niezdolność do właściwego kształtowania analogowych reprezentacji liczby takich jak: wewnętrzna oś liczbowa. Po drugie odnosi się także do zaburzonego rozwoju werbalnych i arabskich wyobrażeń oraz powiązanych z nimi umiejętności obliczeniowych.
Teraz spróbujemy wyjaśnić te fakty a także inne wymienione pojęcia dotyczące DD w obrębie teoretycznego modelu minimalnej kognitywnej struktury zaproponowanej przez Andersona. Rysunek 4 przedstawia trzy podtypy na poziomie dysfunkcji modularnej w obrębie drogi 2 teorii Andersona (Modus 3).
Rys. 4. Teoria minimalnej kognitywnej architektury w kontekście zaburzeń przetwarzania liczby i dokonywania obliczeń
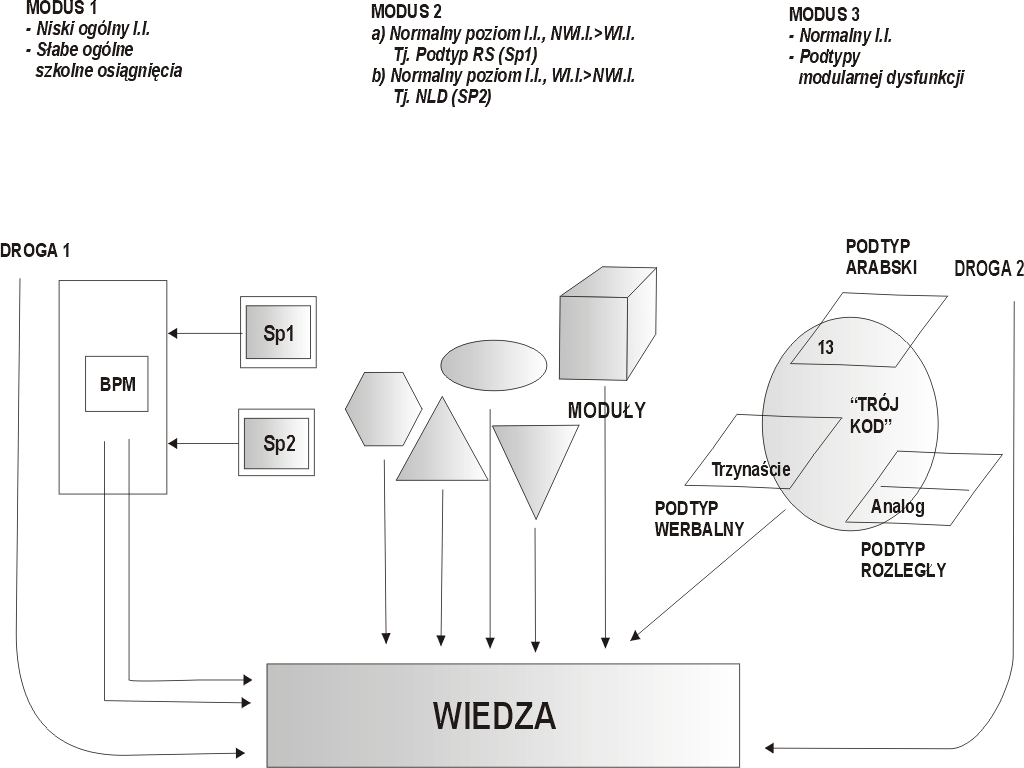
Objasnienia skrótów: NWI.I.-niewerbalny I.I.; WI.I.-werbalny I.I.
W odniesieniu do teorii Fodora i Karmiloffa-Smitha dwa różne rodzaje modułów zostały zaproponowane przez Andersona:
- wrodzony i dany w wyniku presji ewolucyjnej (nazwany "Opcja I");
- nabyty podczas indywidualnego rozwoju zależnie od procesów uczenia się i automatyzacji (nazwany "Opcja II").
Analogiczne wyobrażenie wielkości
z modelu trój-kodowego Dehaene można rozumieć jako moduł typu Opcja-I, a
wyobrażenia werbalnej i arabskiej liczby mogą prawdopodobnie reprezentować
moduły typu Opcja-II. Zatem można wnioskować, że podtyp głęboki, rozległy jest przypuszczalnie
spowodowany przez wpływy genetyczne lub wczesne uszkodzenie mózgu, a podtypy
werbalny (językowy) i arabski są prawdopodobnie spowodowane zaburzeniami rozwoju językowego
wywołanymi wpływami genetycznymi i środowiskowymi. Rozróżnienie Geary pomiędzy
biologicznymi, pierwotnymi i wtórnymi zdolnościami opisuje taki sam warunek
z perspektywy poznawczo - rozwojowej. Biologiczne pierwotne (uniwersalne)
kwantytywne zdolności w koncepcji Geary odpowiadają tym mechanizmom przypisanym
do modułu analogowej wielkości na modelu Dehaene, a biologiczne, wtórne,
odpowiadające kulturowo przekazywanym zdolnościom, mogą odzwierciedlać werbalnemu i arabskiemu
modułowi wyobrażeniowemu.
NLD i podtyp RS dyskalkulii (zobacz wyżej) są najlepiej
znanymi syndromami, które odzwierciedlają półkulową dysfunkcję lateralizacyjną
dla DD, którą można odnosić do specyficznych procesorów (SP1/SP2) w teorii
Andersona (Modus 2 na rysunku 4). Jednak, jak już wcześniej wykazano, słabe
przetwarzanie wzrokowo - przestrzenne, a także słabe przetwarzanie językowe
nie są silnymi predyktorami rozwojowej dyskalkulii. Jednak stanowią czynniki zwiększonego ryzyka. Wydaje się być czymś możliwym do przyjęcia,że słaba sprawność SP1 lub SP2 może poważnie kolidować z procesami modularyzacji: słaba zdolność do przetwarzania poszczególnych jakości informacji (werbalnej/zdaniowej, wzrokowo-przestrzennej/jednoczesnej) może ograniczyć przyswajanie wiedzy i prowadzi do słabej automatyzacji i modularyzacji pewnych zdolności. Ta interakcja może mieć miejsce, na przykład, u dzieci z rozwojowymi zaburzeniami językowymi (słaby SP1). Wiadomo, że dzieci często ujawniają fonologiczną dysleksję, kłopoty w doskonaleniu drugiego języka lub w przetwarzaniu liczby i w arytmetyce szkolnej, prawdopodobnie z powodu zakłóceń dojrzewania modułów językowych. Natomiast dzieci z NLD (cechujące się słabym SP2) mogą wykazywać nieprawidłowości w zakresie modularyzacji poszczególnych zdolności poznawczych, które bazują na mechanizmach wzrokowo-przestrzennego przetwarzania, co często prowadzi do trudności szkolnych takich jak wzrokowo-przestrzenne podtypy dysleksji oraz rozwojowa dyskalkulia. Kiepskie działanie specyficznych procesorów może także zahamowywać modularyzację innych powiązanych z nimi funkcji poznawczych. Na przykład, syndrom NLD był często powiązany nie tylko z DD, ale także z zaburzeniami empatii oraz społecznych interakcji (spektrum autystyczne). Można przypuszczać,że deficyty przetwarzania niewerbalnego, które odzwierciedlają słabą zdolność do rozpoznawania mowy ciała innych ludzi, mogą utrudniać dojrzewanie "teorii umysłu", która przypuszczalnie odgrywa kluczową rolę w rozwoju społecznej kompetencji i która przypuszczalnie jest modularnie uwarunkowana (przez istnienie specifycznych modułów) w teorii Andersona.
Modus 1 na rysunku 4 przedstawia
słabe zdolności matematyczne będące predyktorem słabych ogólnych zdolności
intelektualnych wyrażonych niskim poziomem I.I. Niski I.I. odpowiada słabej
sprawności mechanizmu podstawowego przetwarzania w teorii Andersona.
Dynamika rozwojowa
Trzy moduły wyobrażeniowe zobrazowane na modelu trój-kodowym lub modelu trój kodu przypuszczalnie są funkcjonalnie autonomiczne. Uznając ten model za przedstawiający końcowy etap przetwarzania liczby i dokonywania obliczeń w wieku dorosłym, można będzie dowieść, że te moduły wyłaniają się na różnych etapach rozwoju człowieka. Co więcej, można dowieść, że rozwój modułów oraz sieci neuronów zależy od: (1) pewnych genetycznych predyspozycji (2) specyficznych wpływów środowiskowych (3) rozwojowego postępu, jaki dokonuje się w zakresie sąsiednich modułów liczbowych (M. von Aster, 2000).
Rys. 5. Model obejmujący genetyczne predyspozycje, specyficzne wpływy środowiskowe i rozwój na płaszczyźnie czasowej, jaki dokonuje się w zakresie modułów liczbowych w kontekście dyskalkulii
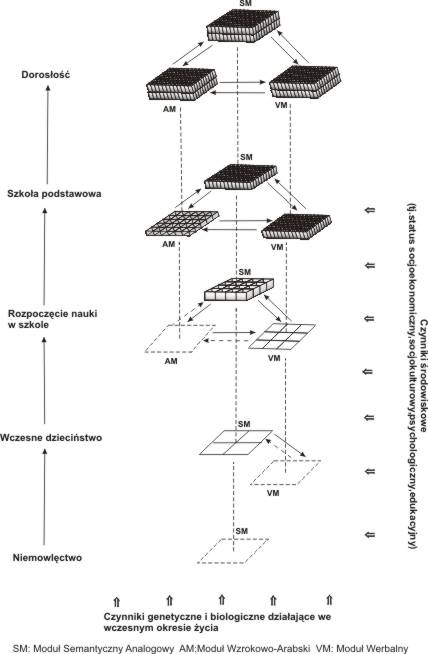
Zespół wrodzonych, prawdopodobnie
uniwersalnych zdolności numerycznych opisanych przez Starkey i in., który
zawiera rdzeń wyobrażenia analogowej semantycznej liczby w teorii Dahaene
wydaje się konieczny do zrozumienia w jaki sposób i dlaczego liczby - słowa
są stosowane oraz do uchwycenia podstawowych zasad liczbowych (porządek rosnący/malejący,
część/całość, ułamek), zasad obliczeniowych i pojęć arytmetycznych. Bez tych semantycznych
podstaw, liczby-słowa, algorytmy arytmetyczne są przyswajane i stosowane jakby nieświadomie, tak naprawdę w niewiedzy na temat tego, co zostało wykonane i z jakiego powodu (M. Von Aster, 2000).
HN był w stanie zrozumieć i stosować
podstawowe zasady liczenia, ale miał poważne trudności w przyswajaniu liczb-słów,
które składały się z więcej niż dwóch elementów sekwencyjnych. Wydaje się,
że miało to miejsce z powodu znacznego, prawdopodobnie także genetycznie
przekazywanego rozwojowego zaburzenia językowego. Dowiedziono, że trudności
doświadczane przez HN są spowodowane defektywnym dojrzewaniem modułu przeznaczonego
do wyobrażenia werbalnej/alfabetycznej liczby. To mogło być szkodliwe dla
dalszego opracowywania analogowych wyobrażeń większych liczb, co znaczyło,
że HN nie udało się wewnętrznie ukształtować i wyobrażać sobie liczb, których
on nie mógł właściwie nazwać. Nie potrafił utworzyć wewnętrznej osi liczbowej
dla większych liczb i, w konskewencji, nie potrafił przetwarzać ich w umyśle
podczas obliczeń. HN mógł, jednak, wytwarzać większe liczby-słowa w momencie,
gdy czytał liczby arabskie, ponieważ przyswoił dobrze zasady notacji i
był w stanie stosować wzrokowo przedstawioną sekwencję cyfr jako pomoc
do poprawnego artykułowania odpowiadającego słowa-liczby. Nie był zaś zdolny do analogicznego uzmysłowienia sobie liczby. Zatem, wypracowywanie analogowych wyobrażeń wydaje się opierać się na właściwych wyobrażeniach językowych. Jednak na zdolność kształtowania takich wyobrażeń mogą mieć także wpływ czynniki środowiskowe, które mogą wyjaśnić różnice kulturowe, tj. różnice między dziećmi europejskimi
a południowo-amerykańskimi podczas ich uczenia się umieszczania liczb na
analogowej osi liczbowej.
Różnorodne czynniki językowe,sekwencje liczb prezentowanych słownie (lub liczebniki) w różnych językach mogą mieć udział w szczególnych trudnościach, które są doświadczane przez dzieci obcojęzyczne lub dwujęzyczne, w nabywaniu arabskiego systemu notacyjnego oraz procedur pisemnego liczenia w środowisku szkolnym. Dzieci te muszą przetwarzać dwie sekwencje liczba-słowo czyli sekwencje liczb prezentowanych słownie. Dzieci dwujęzyczne mogą także ujawniać różne językowe nieprawidłowości w zakresie przekształcenia odpowiedników słownych liczb w językach niemieckim i francuskim (hiszpańskim lub włoskim) na wizualną notację arabską. Te językowe zagubienie, ale i problemy w zakresie orientacji w stronie lewa-prawa oraz zaburzenia przetwarzania przestrzennego, mogą zakłócać proces uczenia się poszczególnych symboli i zasad syntaktycznych notacji arabskiej. W ten sposób mogą przyczyniać się do hamowania dojrzewania modułu arabskiego u dzieci ujawniających wzorzec dyskalkulii podtypu arabskiego.
Konkludując wydaje się, że powstające
i wypracowywane poznawcze wyobrażenia liczby są w połowie-autonomiczne
podczas rozwoju. Każda reprezentacja poznawcza liczby zależy od właściwego przebiegu rozwoju pozostałych.
Czynniki środowiskowe mediacyjne i moderacyjne okazały się mieć udział w indywidualnych różnicach w zakresie czynności i działań matematycznych. Czynniki, które cieszą się szczególnym zainteresowaniem w dyskusji nad rozwojem matematycznym i DD to płeć, interakcje między funkcjonowaniem edukacyjnym a psychospołecznym, wpływ klasy społecznej i środowiska kulturowego, a także formalna edukacja i metody nauczania.
Wskaźniki rozpowszechnienia dla DD przyjmują wyższe wartości dla dziewcząt niż dla chłopców, co wydaje się odzwierciedlać znaczenie płci dla rozwoju umiejętności matematycznych. Fakt, że uwidocznienie tego skutku jest wysoce zmienne w zależności od kraju świata oraz, że wpływ ten zmniejszył się w ostatnich dekadach, wskazuje,że prawdopodobnie nie można tego wyjaśnić tylko czynnikami biologicznymi. Kilka alternatywnych hipotez przyjęto, by wyjaśnić wpływ wywierany przez płeć. Różnice między chłopcami i dziewczętami w postawach, samoocenie oraz specyficznym lęku mogą pełnić ważną rolę w kształtowaniu się umotywowanego i celowego uczenia
się. ĺrodowisko edukacyjne oraz metody nauczania mogą także nieznacznie faworyzować chłopców wtedy, kiedy niewłaściwie odzwierciedlają one różnice w stylach poznawczych, myśleniu algorytmicznym i preferowanych środowiskach dydaktycznych przez chłopców i dziewczęta.
U dzieci z DD, objawy behawioralne i emocjonalne, a także często współistniejące trudności w uczeniu się, czasami poprzedzają doświadczanie niepowodzeń szkolnych, co dobitnie wykazano w indywidualnym studium przypadku HN. Ilość i nasilenie zaburzeń współistniejących mają silną wartość prognostyczną dla globalnego przystosowania osobowościowego oraz osiągnięć szkolnych. Wczesna diagnoza i wczesna interwencja, dopasowane do zróżnicowanego oszacowania kłopotów są niezbędne, aby zapobiegać skutkom psychospołecznym wywieranym przez syndrom NLD.
LITERATURA:
Von Aster M. (2000). Developmental cognitive neuropsychology of number processing and calculation: varieties of developmental dyscalculia. European Child&Adolescent Psychiatry, 9, 41-57.